复合结构（复合管、复合缆）的力学行为计算通常非常复杂，涉及多种材料、结构及界面接触，因此，在工程中往往需要更简单的等效计算方法来对复合结构的各种物理行为（如力学、热力学等）进行快速估算。

一个代表性的案例是：求解由多根金属丝组成的大复合缆的抗弯刚度（bending stiffness），此时需要考虑缆的结构和金属丝之间的耦合情况。抗弯刚度通常表示为EI，其中E 是弹性模量，I 是截面惯性矩。以下是基于不同情况的求解方法：

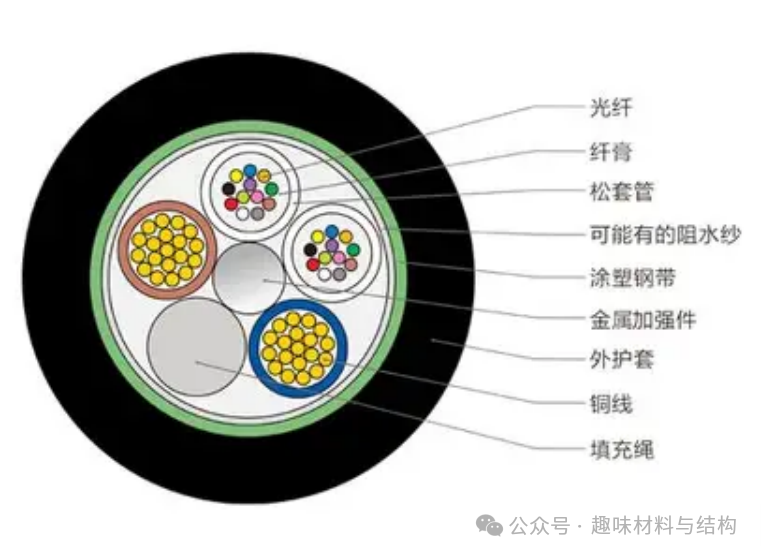
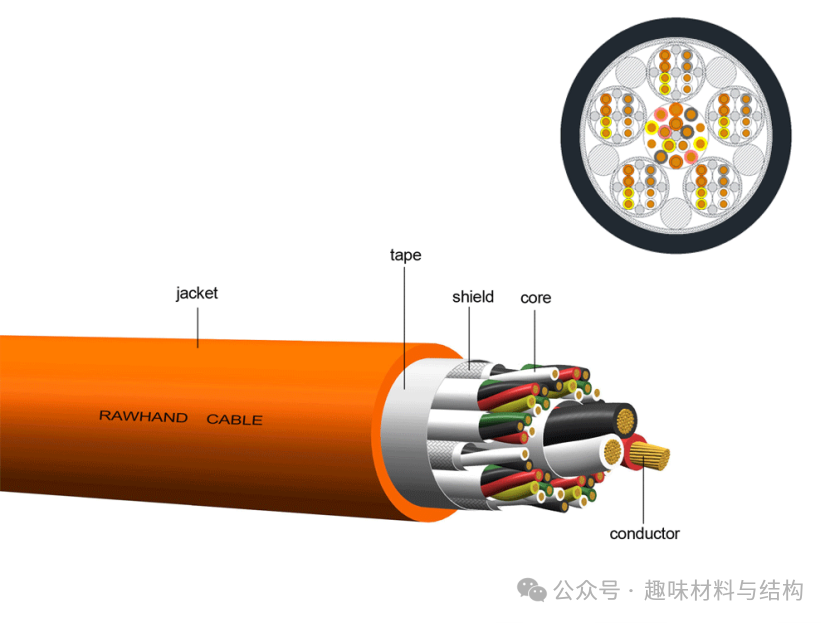
1. 金属丝通过基体材料粘结（如复合材料）

如果金属丝嵌入在基体材料（如环氧树脂）中，并完全粘结在一起，复合缆可以视为一个整体梁。抗弯刚度计算如下：

- 等效弹性模量 E_composite：使用混合法则计算：

其中：

- V_f 是金属丝（纤维）的体积分数

- E_f 是金属丝的弹性模量

- V_m 是基体材料的体积分数

- E_m 是基体材料的弹性模量

- 整体截面惯性矩 I_composite：如果缆的截面是圆形，且外径为D，则：

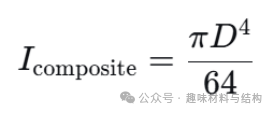
- 抗弯刚度：

2. 金属丝机械绞合，无粘结（如钢丝绳）

如果金属丝仅通过机械绞合在一起，没有基体材料粘结，抗弯刚度取决于金属丝之间的摩擦和绞合角度。这时，有效抗弯刚度通常低于整体计算值，因为金属丝在弯曲时可能发生相对滑动。

以下是常用方法：

- 方法一：基于单根金属丝的求和（下限值）

- 计算单根金属丝的截面惯性矩 I_single（假设金属丝为圆形截面）：

其中 -d 是单根金属丝的直径。

- 抗弯刚度：

其中n 是金属丝的数量。这种方法假设金属丝完全独立弯曲，但实际中由于摩擦，刚度可能稍高。

- 方法二：基于几何惯性矩的经验公式（更实用）

- 计算缆的整体几何惯性矩 I_geom（基于外径D）：

- 抗弯刚度：

其中：k 是一个经验系数，通常介于 0.5~0.8 之间，取决于缆的绞合角度、金属丝之间的摩擦和缆的构造。对于绞合角 α，k 可能随 sin²(α) 减小。具体值需参考制造商数据或实验测定。

3. 考虑金属丝分布的计算（如果金属丝位置已知）

如果金属丝在截面中的分布已知，可以计算整体惯性矩：

- 首先找到缆的形心（通常为几何中心）。

- 整体惯性矩 I_total为每根金属丝自身惯性矩和并行轴定理贡献之和：

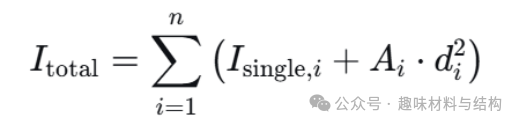
其中：

- I_single,i 是第 i 根金属丝的自身惯性矩，

- A_i 是第i 根金属丝的截面积（A_i = πd²/4），

- d_i 是第i 根金属丝中心到形心的距离。

- 抗弯刚度：

这种方法适用于金属丝粘结或紧密绞合的情况，但可能高估实际值如果金属丝滑动。

4.并行轴定理

并行轴定理，也称为平行轴定理或惠更斯-斯坦纳定理。

1) 核心概念与定义

并行轴定理描述了刚体对于任意轴的转动惯量（或称惯性矩）与对于通过其质心的平行轴的转动惯量之间的关系。

核心思想：

一个形状对于某个轴的惯性矩，等于它对于通过其自身形心的平行轴的惯性矩，加上该形状的面积（或质量）与两轴之间距离平方的乘积。

2) 数学表达式

对于面积惯性矩（在结构力学和抗弯刚度计算中常用），其公式为：

其中：

- I：是刚体对于目标轴（任意轴）的惯性矩。

- I_c：是刚体对于通过其形心且与目标轴平行的轴的惯性矩。这是物体自身的、固有的惯性矩。

- A：是刚体的面积。

- d：是目标轴与通过形心的平行轴之间的垂直距离。

对于质量惯性矩（在动力学中常用），公式类似：

其中：

m 是质量；

J和J_c是相应的质量惯性矩。